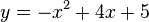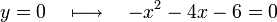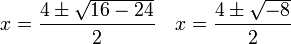ALGEBRA 2011: FUNCION CUADRATICA

En matemáticas, una función cuadrática o función de segundo grado es una función polinómica de grado dos definida como:

$f(x) = ax^2 + bx + c \,$

en donde a, b y c son números reales (constantes) y a es distinto de 0.

La representación gráfica en el plano XY haciendo:

$y = f(x) \,$

esto es:

$y = ax^2 + bx + c \,$

es una parábola vertical, orientada hacia arriba o hacia abajo según el signo de a.

Corte con el eje y

La función corta el eje y en el punto y = f(0), es decir, la parábola corta el eje y cuando x vale cero (0):

$y = f(0) = a \cdot 0^2 + b \cdot 0 + c \,$

lo que resulta:

$y = f(0) = c \,$

la función corta el eje y en el punto (0, c), siendo c el termino independiente de la función.

lo que resulta:

$y = f(0) = c \,$

la función corta el eje y en el punto (0, c), siendo c el termino independiente de la función.
A este punto de la función también se lo conoce con Ordenada al Origen

Corte con el eje x

La función corta al eje x cuando y vale 0, dada la función:

$y = ax^2 + bx + c \,$

tendremos que:

$y = 0 \quad \longmapsto \quad ax^2 + bx + c = 0 \,$

las distintas soluciones de esta ecuación de segundo grado, son los casos de corte con el eje x, que se obtienen como es sabido por la expresión:

$x = \frac{-b \pm \sqrt{b^2 - 4 a c}}{2 a}$

donde:

$b^2 - 4 a c \,$

se le llama discriminante, Δ:

$\Delta = b^2 - 4 a c \,$

según el signo del discriminante podemos distinguir:

Discriminante positivo

Δ > 0, la ecuación tiene dos soluciones, y por tanto la parábola cortara al eje x en dos puntos:

x 1

x 2

Veamos por ejemplo la función:

$y = -x^2 + 4x + 5 \,$

que cortara el eje x cuando:

$y = 0 \quad \longmapsto \quad -x^2 + 4x + 5 = 0 \,$

que tendrá por solución general:

$x = \frac{-b \pm \sqrt{b^2 - 4 a c}}{2 a}$

en este caso:

$x = \frac{-4 \pm \sqrt{4^2 - 4 (-1) 5}}{2 (-1)}$

que resulta:

$x = \frac{-4 \pm \sqrt{16 + 20}}{-2}$

Para esta ecuación el discriminante tiene valor positivo:

$\Delta = 16 + 20 = 36 \,$

y por tanto tiene dos soluciones:

$x_1 = \frac{-4 + \sqrt{36}}{-2} \quad x_2 = \frac{-4 - \sqrt{36}}{-2}$

operando:

$x_1 = \frac{-4 + 6}{-2} \quad x_2 = \frac{-4 - 6}{-2}$

$x_1 = \frac{2}{-2} \quad x_2 = \frac{-10}{-2}$

$x_1 = -1 \quad x_2 = 5$

Los puntos: (-1,0), (5,0) son los de corte con el eje x, como se puede ver en la figura.

Discriminante nulo

Δ = 0, la ecuación tiene una única solución en

x 1

, la parábola solo tiene un punto en común con el eje x, el cual es el vértice de la función donde las dos ramas de la parábola confluyen.

si la función cuadrática:

$y = -x^2 + 4x - 4 \,$

que cortara al eje de las x si:

$y = 0 \quad \longmapsto \quad -x^2 + 4x - 4 = 0 \,$

su solución sera:

$x = \frac{-b \pm \sqrt{b^2 - 4 a c}}{2 a} \quad x = \frac{-4 \pm \sqrt{4^2 - 4 (-1) (-4)}}{2 (-1)}$

Operando los valores, tendremos:

$x = \frac{-4 \pm \sqrt{4^2 - 16}}{-2} \quad x = \frac{-4 \pm \sqrt{0}}{-2}$

la raíz de cero es cero, luego el discriminante en este caso vale cero, y habrá una única solución:

$x_1 = x_2 = \frac{-4}{-2} = \frac{4}{2} = 2$

El punto de corte de la función con el eje de las x es (2,0), que en este caso es tangencial de la función con el eje, ver figura.

Discriminante negativo

Δ < 0, la ecuación no tiene solución real, y la parábola no corta al eje x.

Si tenemos la función siguiente:

$y = - x^2 - 4x - 6 \,$

que corta el eje x cuando:

$y = 0 \quad \longmapsto \quad - x^2 - 4x - 6 = 0 \,$

para encontrar su solución haremos:

$x = \frac{-b \pm \sqrt{b^2 - 4 a c}}{2 a} \quad x = \frac{-(-4) \pm \sqrt{(-4)^2 - 4 (-1) (-6)}}{2 (-1)}$

Haciendo las operaciones, tendremos:

$x = \frac{4 \pm \sqrt{16 - 24}}{2} \quad x = \frac{4 \pm \sqrt{-8}}{2}$

Al no existir ningún número real que sea la raíz de –8, no se puede continuar haciendo las operaciones, por lo que podemos decir que esta función no tiene corte con el eje x, como se ve en la figura.
Si tenemos en cuenta la existencia de los números imaginarios, podemos realizar las siguientes operaciones:

$x = \frac{4 \pm \sqrt{8(-1)}}{2} \quad x = \frac{4 \pm \sqrt{8} \, \sqrt{-1}}{2} \quad x = \frac{4 \pm \sqrt{8} \; i }{2}$

Continuando con las operaciones:

$x = \frac{4}{2} \pm \frac{\sqrt{8} \; i}{2} \quad x = \frac{4}{2} \pm \sqrt{\frac{8}{4}} \; i \quad x = 2 \pm \sqrt{2} \; i$

dando como solución:

$x_1 = 2 + \sqrt{2} \; i$

$x_2 = 2 - \sqrt{2} \; i$

Dado el plano cartesiano xy, real, la parábola vista no corta el eje real x en ningún punto, esa misma ecuación estudiada dentro de los números complejos presenta dos soluciones, cumpliéndose de este modo el Teorema fundamental del álgebra.
A la/s intersección/es de la gráfica de la función con el eje x se las llama Ceros o Raíces de la función